Introduction
Network Topologies
A network topology is the arrangement of elements in a computer network. Each network topology has its advantages and disadvantages and as new topologies are adopted older topologies are depreciated(no longer recommended and their use slowly discontinued).
Older topologies that are no longer widely used include Ring and Bus networks.
Physical vs Logical Topology
A network topology can be used to represents networks both physically and logically.
- Logical Topology – How elements are connected in principle, though the physical connection may differ
- Physical Topology – How elements are actually plugged in together in reality.
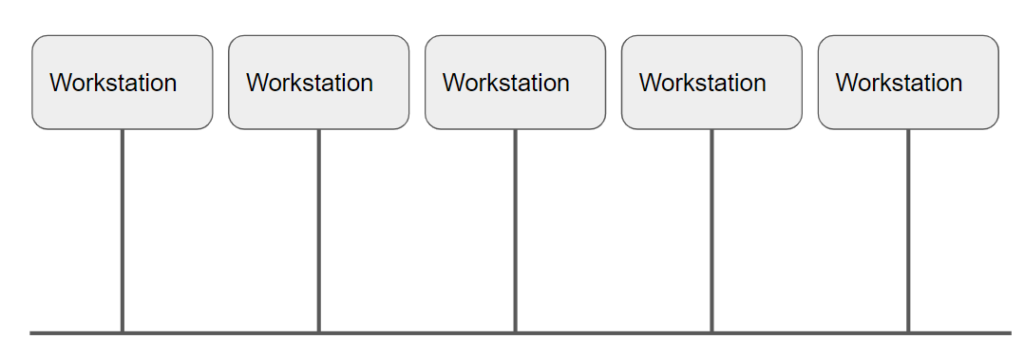
Bus
Bus Topology
A bus topology uses a single coaxial trunk cable that runs between all the nodes on the network. When a new node is added a t-connector is used to connect the new node to the cable.
Advantages
- Very quick to setup
- Cheap to implement
Disadvantages
- If there is a break in the cable or if a node goes down then the network is split in two and may no longer function.
- The main cable can run into bandwidth issues as all data travels down the backbone.
Ring
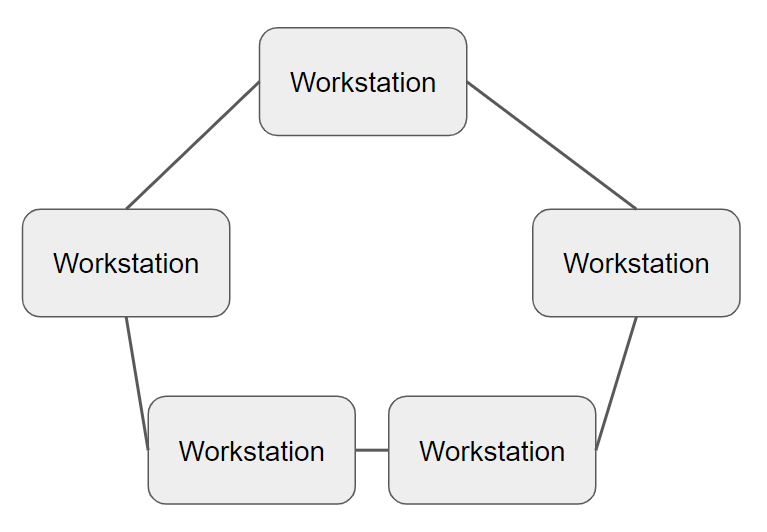
Ring Topology
In a ring network all computers have two network connectors and each connector runs either clockwise or anticlockwise onto the next node.
Advantages
- Simple to set up
- Cheap to install
Disadvantages
- If one part of the cable breaks the entire network goes down.
Mesh
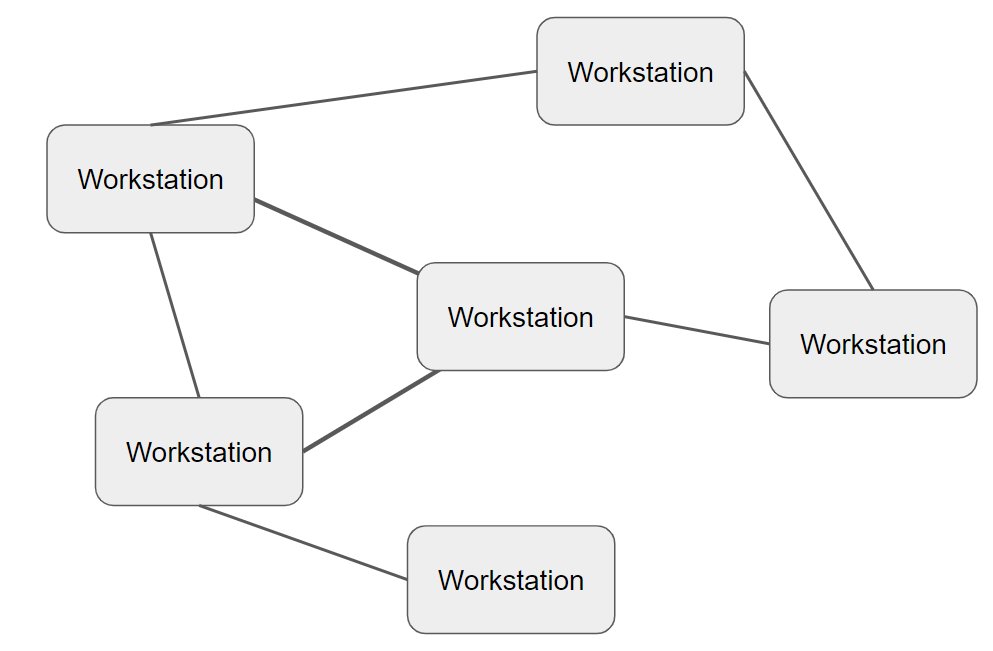
Mesh Topology
A mesh topology is mostly used in ad-hoc networks or home networks. Their is no specific structure and all nodes can connect directly together or indirectly through other nodes.
There are two types of mesh topology: full mesh and partial mesh.
- In a full mesh all nodes are connected to each other
- In a partial mesh only some of the nodes are connected together
- Peer to Peer sharing networks are generally logical mesh networks.
Advantages
- Easy to set up as little planning is required
- If one node goes down the rest of the network can carry on functioning.
Disadvantages
- Difficult to manage and troubleshoot.
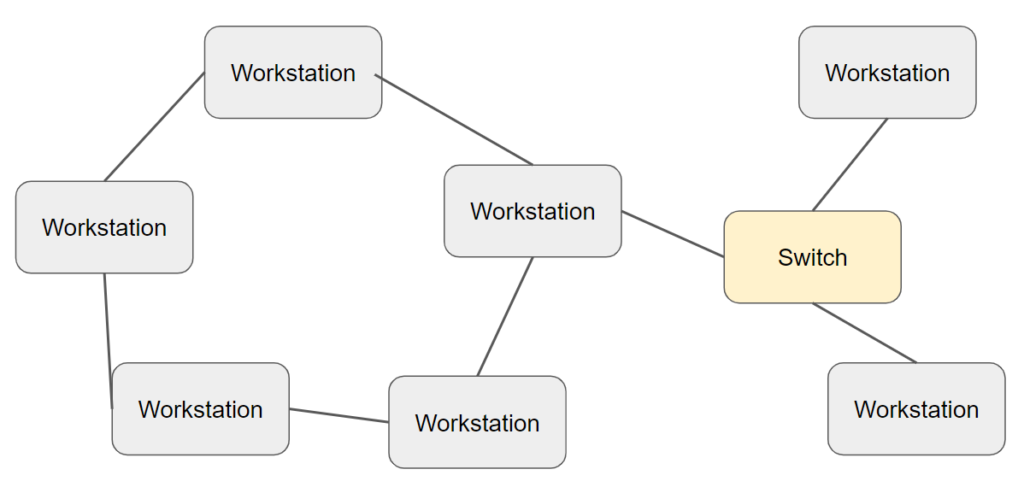
Star
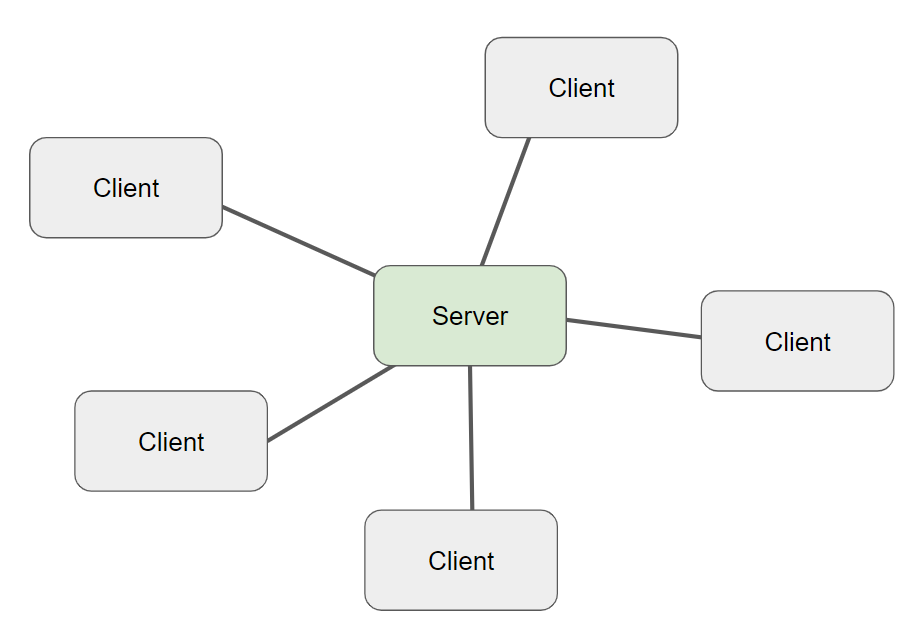
Star Topology
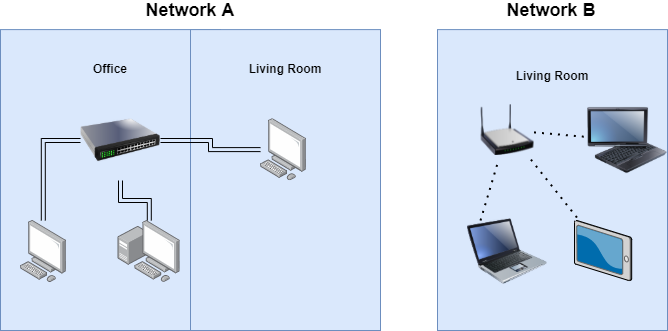
In this topology infrastructure network all clients(workstations) connect to a central server. This is the most common topology for business and office environments.
Advantages
- If a cable breaks then only one device loses network access
- Easy to maintain and debug
- Client-Server Model allows management of all devices
Disadvantages
- This network type requires more hardware than other types and therefore it is more expensive to install.
Hybrid
Hybrid Topology
Hybrid topologies are adapted to the particular needs of a network. The strengths and weaknesses are a mixture of the topologies that make up the network.