Hexadecimal Number System - A Level Computer Science

Intro

What is Hexadecimal?

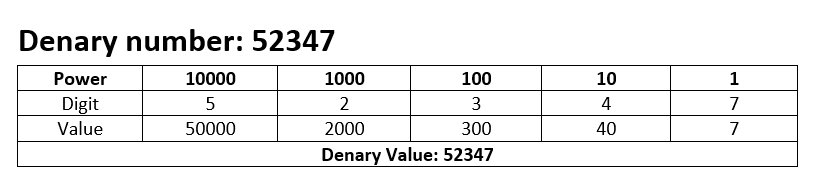
In the normal human counting system we use a base 10 number system, meaning that the each extra digit increases in powers of 10 each time:

Hexadecimal is a Base 16 number system, meaning that increases in powers of 16, with each digit being one of 16 different combinations.

The hexadecimal number consists of:

0 = 0
1 = 1
2 =2
3 = 3
4 = 4
5 = 5
6 = 6
7 =7
8 = 8
9 = 9
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

Why do we use a to f instead of 11 to 15?

We can’t use 11 to 15 because we wouldn’t know what number it represented. The Digits 13 could be 13 or it could be 19 (1 * 16 + 3), this is because denary numbers greater than 9 use 2 digits instead of one digit.

Why do we use it hexadecimal?

Given how confusing hexadecimal is you might be forgiven for wondering why we bother using it at all. Well it has a couple of advantages:

Large numbers can be represented in a smaller number of digits, making them easier and more accurately read by humans.

Binary is very difficult for humans to read (especially larger numbers) but computers work in binary, so any usage where you need to be able to inspect and edit the binary directly (such as in machine code/ assembly language) humans can work in hexadecimal, which is close to the binary representation, but easier for us to read.

The reason Hexadecimal works so well with binary is because of the similarity between the number systems.

binary base 2 –> 2 to the power of 4 is 16, so ever 4 binary digits are equal to one hexadecimal digit. This makes conversion really easy!!!!