Introduction
Why do errors occur?
When data is transferred through a network at each stage there is possibility that data might get corrupted. Therefore when a packet is received it needs to be checked to ensure the integrity of the data. Two common ways this can be achieved is through the use of parity bits and check-sums.
Parity Bit
Parity Bit (Aka Check Bit)
A check bit is a simple method of error checking used to detect data corruption of small blocks of data (usually at byte level) during storage or transmission of data. A single bit of data is added to a string of bits and order to ensure that the sum of the total of bits is either even or odd.
- If even parity is used then sum of the digits must add up to an even number
- If odd parity is used the sum of the digits must add up to an off number
After the data is transmitted, the receiving device adds up the string of bits again (this time including the added bits) and checks it for parity.
If the received data does not match the required parity then the data is corrupt and must be re-sent.
Example(using even parity)
| Original 7-bit binary data | 0110101 |
| Binary data with 0 parity bit added | 01101010 |
| Example received data (corrupted) | 01001010 (Now odd number of 1s) |
In the example above the 7 original bits added up to an even number, so a 0 was added to the end. When the data was received the number now added up to an odd number, so the data must have been corrupted during the transmission process.
Limitations of parity bits
A parity bit check is not perfect and some errors are still possible (for example if 2 bits have been corrupted)
Check Digits
Check Digits
A check digit is a single digit number that is added to the end of a string of digits to detect human error during manual entry, such as entering a wrong digit or reversing two digits when entering a credit card on a shopping website.
Check digits are commonly used on:
- Barcodes
- Credit Cards
- Account Numbers
- Government ID Numbers
Luhn's Algorithm
Luhn’s Algorithm
Luhn’s algorithm is a simple mathematical technique that used modulo to detect simple errors. It is commonly used on 15 digit credit card numbers to automatically calculate the 16th digit.
The technique is simple.
Write all the digits down in order.
- For each number in the sequence that is in an odd position (first, third, fifth,etc) multiply that number by two and add each of the digits of the result together.
- For each number in the sequence that is in even position, leave it as is.
- Now add up all the resultant numbers together (including the ones you left as is)
- Work out 10 minus modulo 10 of the total ( = 10 – Total MOD 10 )
- The answer is the 16th digit!
Barcodes use a mod 10 algorithm with a 3x multiplier instead of a 2x
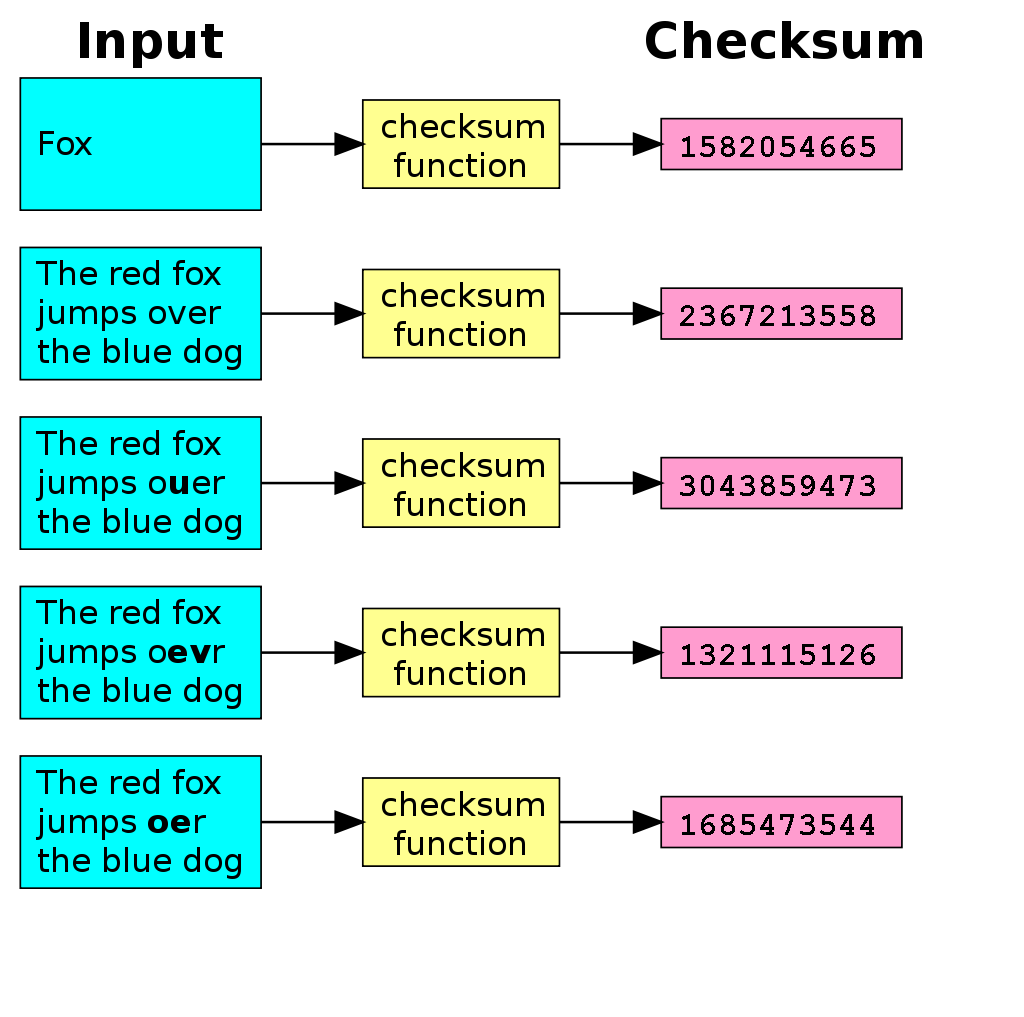
Check sums
Check Sums
Check sums are used to detect accidental corruption of large blocks of data after transmission of storage. They are commonly used to verify the integrity of downloaded files or programs after downloading them from the internet.
The use more complex algorithms than check digits or parity bits and the resultant sum is much larger in size. While checksums do not 100% guarantee the integrity of data ensure a very high probability of corruption detection.
Resources
Resources
Past Paper Questions
0478/12 Paper 1 Theory May/June 2015 – Qn 5
0478/11 Paper 1 Theory May/June 2016 Qn 9
0478/12 – Paper 1 Theory May/June 2016 Qn4b
0478/11 – Paper 1 Theory October/November 2016 45d
0478/12 – Paper 1 Theory October/November 2016 Qn4