Introduction
What is binary?
Binary is a base 2 number system, meaning that all numbers and other data can only represented using ones and zeros. All modern computer systems store data and programs in binary.
Why binary?
Why do computers use binary?
There are a number of advantages to using binary in computer systems:
Key Advantages
- Binary data can be transmitted easily and reliably.
- Binary data can be stored and read very easily and reliably.
- Computers use circuits that can only be on one of 2 states – on or off, these work very well with binary calculations.
- The input voltage in to computers is not very stable, so only a system that use voltage/no voltage would be reliable.
Take a look at the following video for more detailed information.
YouTube blocked at school? Watch the Google Drive version instead.
Bits, Bytes, Nibbles
Bits, Bytes & Nibbles
Bit – e.g. 0
Each individual 1 or 0 is known as a bit.
Here are three bits – 110
Byte – e.g. 11001100
Each group of 8 bits is known as a Byte
Here is a stream of Bytes:
01010011 01101011 01111001 01110010 01101001 01101101 00100000 01101001 01110011 00100000 01100001 01110111 01100101 01110011 01101111 01101101 01100101 00100001
Nibble – e.g. 1111
A nibble is 4 bits, or half a Byte.
Here is a nibble – 1101
Denary to Binary
Decimal to Binary Conversion
Let’s suppose we are trying to find the binary for the decimal number 75.
Step 1 – Write the 128 to 1 numbers
Starting on the right hand side, write down the numbers 1, 2,4,8 etc, doubling each time until you reach 128.
Remember smallest number at the right hand side!!!
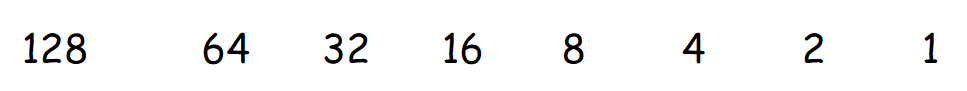
Step 2 – Cross out the unused numbers
Keeping only the numbers that you need to add up to your decimal number, cross out all other numbers.
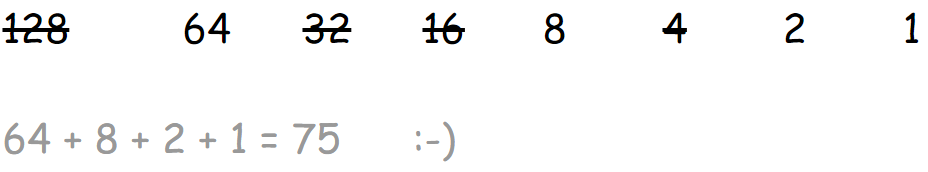
Step 3 – Write the ones or zeros
Under each number write a 1 if there is a number and a zero if you crossed out the number. Put the numbers all together and you have your binary number!

Binary to Denary
Binary to decimal Conversion
Let’s suppose we are trying to find the decimal for the binary number 01101011.
Step 1 – Write the 128 to 1 numbers
Starting on the right hand side, write down the numbers 1, 2,4,8 etc, doubling each time until you reach 128.
Remember smallest number at the right hand side!!!
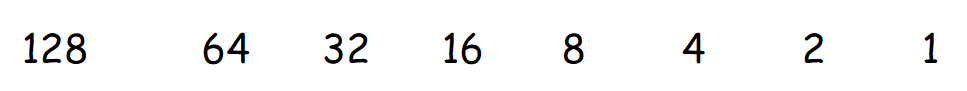
Step 2 – Write the ones and zeros below the numbers
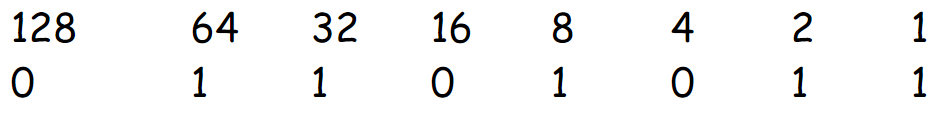
Step 3 – Add up all the numbers with 1s below them to find your decimal number
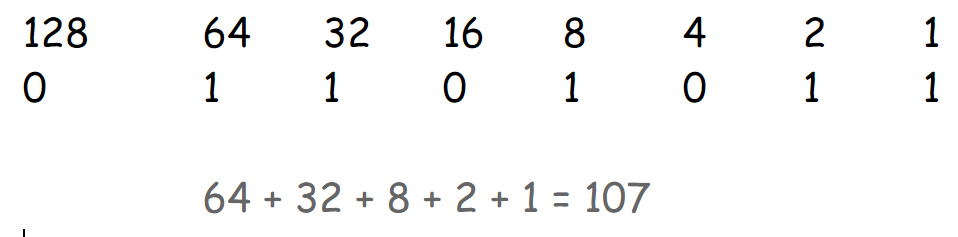
Practice
Practice
Practice converting denary to binary with the great little game.
