Merge Sort

Introduction to Merge Sort

Merge Sort is a popular sorting algorithm that follows the divide and conquer approach. The algorithm works by breaking down the list into smaller sub-lists and sorting them individually.

These sorted sub-lists are then merged back together to obtain the final sorted list.

Time & Space Complexity

• Merge sort is a divide and conquer algorithm, it has a logarithmic time complexity of  O(n log n)
• Merge sort’s space complexity is O(n)

Steps of Merge Sort

1. Divide the unsorted list into smaller sub-lists until each sub-list contains only one element.
2. Repeatedly merge adjacent sub-lists to produce new sorted sub-lists until there is only one sub-list remaining. This is done by comparing the elements of the sub-lists and merging them in the correct order.
3. The final sorted list is obtained when all sub-lists are merged.

Source: Wikipedia

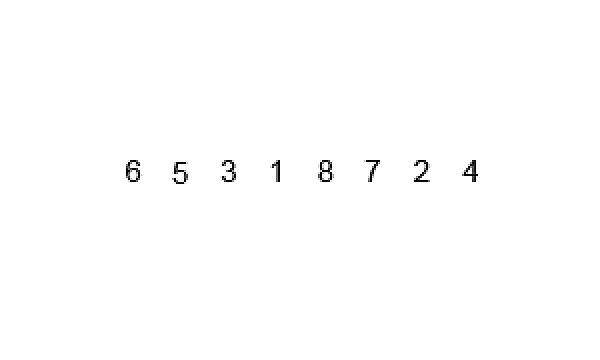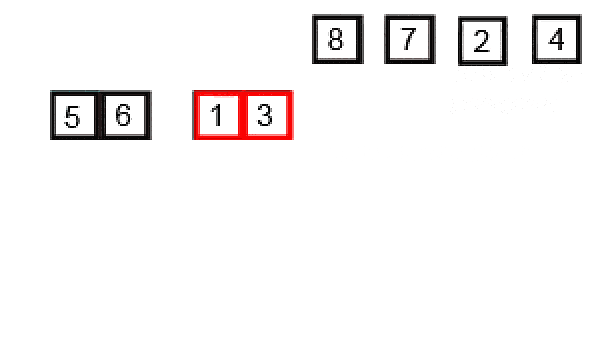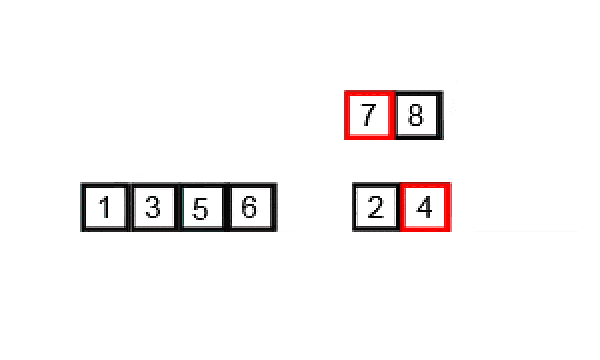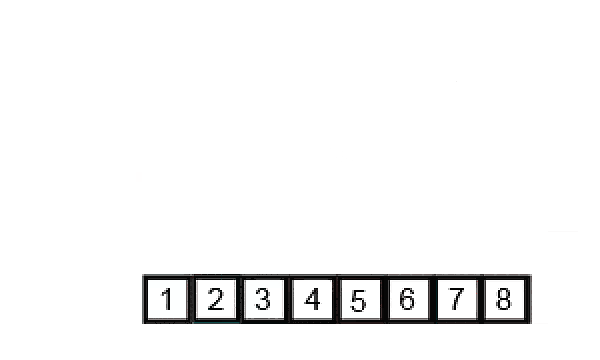
Advantages of Merge Sort

• Merge Sort guarantees a stable sort, which means that the order of equal elements is preserved.
• It performs well on large lists and has a time complexity of O(n log n), where n is the number of elements in the list.

Disadvantages of Merge Sort:

• It is not an in-place sorting algorithm, meaning it needs extra storage proportional to the size of the input list.
• Because it is usually implemented using recursion it can be difficult for beginner programmers to implement and understand.