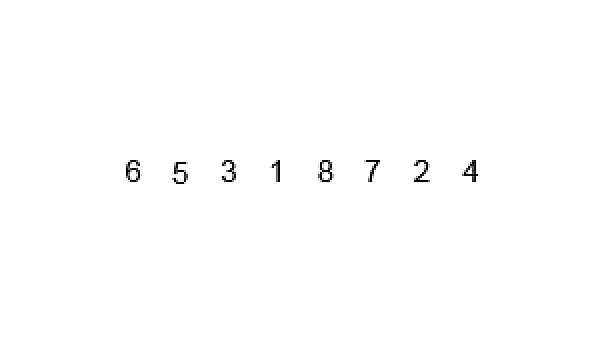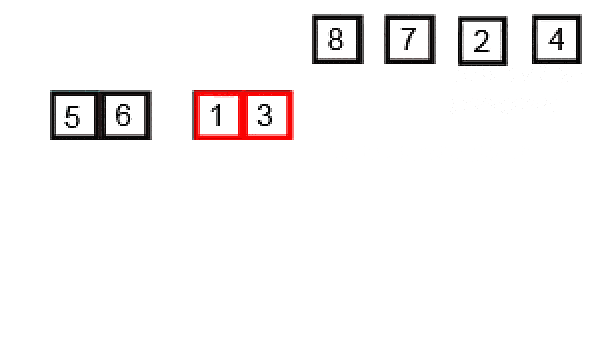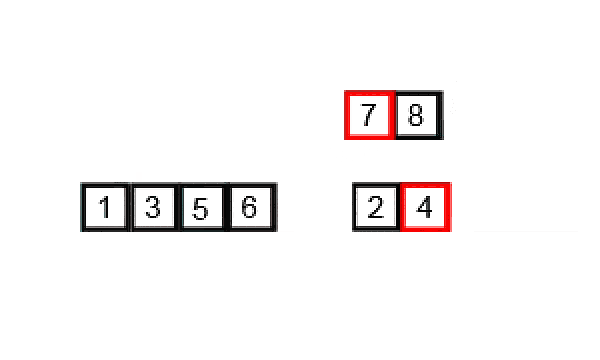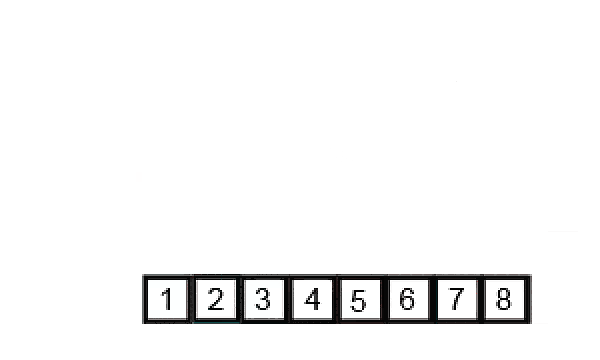Merge Sort
Merge Sort
Time Complexity: O(n log(n)) – Space Complexity: O(n)
Merge Sort is a popular sorting algorithm that follows the divide and conquer approach. The algorithm works by breaking down the list into smaller sub-lists and sorting them individually.
Merge sort steps
- Divide the unsorted list into smaller sub-lists until each sub-list contains only one element.
- Repeatedly merge adjacent sub-lists to produce new sorted sub-lists until there is only one sub-list remaining. This is done by comparing the elements of the sub-lists and merging them in the correct order.
- The final sorted list is obtained when all sub-lists are merged.
Source: Wikipedia
Pros & Cons
Python Code
Python Code
def merge_sort(arr): if len(arr) <= 1: return arr # Split the array into two halves mid = len(arr) // 2 left_half = arr[:mid] right_half = arr[mid:] # Recursively sort both halves left_half = merge_sort(left_half) right_half = merge_sort(right_half) # Merge the sorted halves return merge(left_half, right_half) def merge(left, right): merged = [] left_index, right_index = 0, 0 while left_index < len(left) and right_index < len(right): if left[left_index] < right[right_index]: merged.append(left[left_index]) left_index += 1 else: merged.append(right[right_index]) right_index += 1 # Append any remaining elements from both lists (if any) merged.extend(left[left_index:]) merged.extend(right[right_index:]) return merged # Example usage: arr = [12, 11, 13, 5, 6, 7] sorted_arr = merge_sort(arr) print("Sorted array:", sorted_arr)
Video