Logic Statements & Truth Tables

Logic Statements

Logic statements, also known as logical statements or propositions, are declarative sentences that express a specific truth value. They can be either true or false, but not both simultaneously. Logic statements are fundamental building blocks of logic and are used to construct logical arguments and reasoning.

They can written is a wide number of ways but in your exam you will likely come across the following 3 styles and usually you will be asked to construct either a truth table or a logic circuit from the logic statement.

• Logic Statements using ifs and 1s/0s
• Logic statements written as an equation
• Logic statements written as a natural language sentence

Logic Statements using ifs and 1s/0s

This is basically an equation written using simple more simple natural language

Example

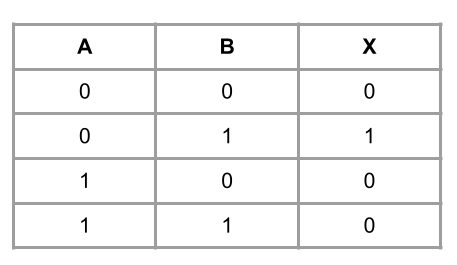
X = 1 if input A is 0 and input B is 1

Truth table

The truth table for the above example would look like this:

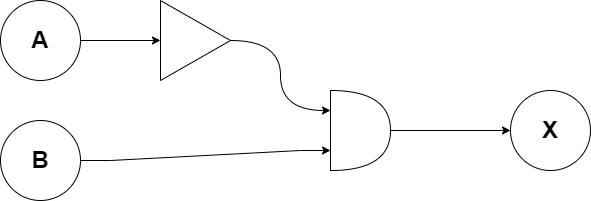
Logic Circuit

The simplest form of logic circuit representation would look like this:

 

Logic statements written as an equation

This is where a logic statement is expressed using standard mathematical notation,

Example: Q = (NOT A) AND B

 

Logic statements written as a natural language sentence

Here a logic statement is written as a normal sentence, often applied to a read-world scenario.

• Xavier will attend the party if Amy isn’t going and Bethany is going.

 

Practice

Can you draw the truth tables and logic circuits for the following examples?

1. X = 1 if input A is 0 or input B is 0
2. X = 1 if input A is 1 or input B is 0, but only if input C is 0
3. Q = (A AND B) OR (NOT B)
4. Q = (A OR B) AND (A AND (NOT B))
5. A chick incubator alarm(X) is activated if the temperature is too high(A), too low(B) and the manual override switch(C) is disabled.
6. Sarah(S) wears a coat to school if it is rainy(R) or cold(C), but not if she is taking the bus.

 

Resources